I-V Characteristic of a Solar Cell

Now that we know a bit about the physical processes behind photovoltaic energy conversion, let’s take a look at the device that does this, a solar cell. In the next few posts, we will go deep into all the operating principles of solar cells. We will discuss the semiconductor physics and optics governing their behavior and you will really get a sense of how solar cells work.

Nevertheless, let’s start by trying to understand an important aspect for any electrical component, the current-voltage or “i-V” characteristic of the solar cell. Here we see a basic solar cell schematic. There are many different components and layers and you will become familiar with the properties and purposes of all these layers throughout the blog.

All you need to know for this post is that a solar cell can take energy from illumination, and convert it into electrical energy in an external circuit. This post’s objective is to answer ‘what’. You will need to go through the rest of the course to understand ‘why’ and ‘how’.in this post, I will quickly explain to you what the current-voltage characteristic of a solar cell is.

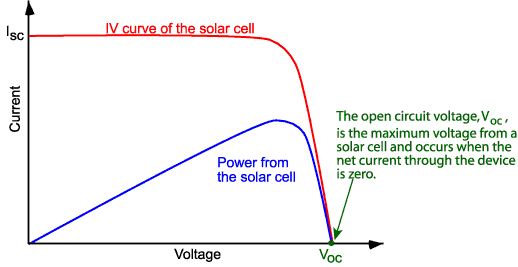
We will try to understand some basic parameters of a solar cell. Here we can see a typical current vs voltage characteristic of a solar cell under illumination. We will delve further into how the calculate this curve in later posts, but now we can just look at some important parameters of the curve. First off we can see that the curve passes through the x-axis. Since current is 0 at this point, this point essentially represents the voltage a solar cell would exhibit when disconnected from any external circuit. As such, we call this point the open circuit voltage or “V_OC”. Similarly, we can see the crossing of the curve along the y-axis.

This point is equivalent to short-circuiting the solar cell as the voltage on either electrode of the solar cell is equal. As such, we call this the short circuit current or “i_SC”. Let’s look at this curve a little further and consider the power output of a solar cell. You should know that power is equal to the product of current and voltage. We will represent the product of the open circuit voltage and short circuit current with a yellow box. This power is greater than the maximum power that a solar cell can produce, however, it will be useful to calculate the solar cell’s efficiency. Now we can see the power as a function of voltage.

We can see that there is a point where the power generated by the solar cell is maximized. We call this our maximum power point. The voltage at this maximum power point is given here as “V_MP” and the current as “i_MP”. You can see that V_MP is less than V_OC and i_MP is less than i_SC. This is always the case. The product of V_MP and i_MP gives the maximum power we can generate, which we denote here as “P_Max”.

We define the ratio of P_MAX to the product of V_OC and I_SC as the Fill Factor or “FF”. The fill factor essentially shows the quality of our solar cell. A greater fill factor implies a greater fraction of that theoretical power can be produced. With these terms, we can define our conversion efficiency, “eta”. The efficiency of any such system is first defined by the power output divided by the input power, which we will call “P_i”.With these equations you can see that we can call the maximum power output, simply P_max.

We could also define it as the product of V_MP and i_MP. Finally, we can also use the V_OC, i_SC and the fill factor. All of these terms are equal. You should now understand the I-V characteristic of a solar cell. You know the basic external parameters, V_OC, i_SC and fill factor and how to calculate the efficiency based on these values. In the next post, we will learn how to model this i-V behavior with electrical components in an equivalent circuit.